Part 1 Ė Time based motion
Introduction
Have you ever played a
very old game to discover that it runs so ridiculously fast that you cant play it? Wondered why it happened? I will tell you that
and how to avoid that your game acts like that on fast computers. The reason
why it happens is that the game is made for a slower computer then yours. The
fps gets too high when itís running on faster computers. Donít worry, there are some ways around this. The first way is to
limit the max fps. This is good, but you need to be sure that every computer is
fast enough to run it at that framerate(or, better, a
higher framerate). When you execute it at slower computers, you get an slow and inconsequent fps. To avoid this you can heavily
optimize your program, or you can use time based motion instead of limiting the
fps. This wonít get you a higher fps on slow computers, but makes sure that
your movement is ďfittingĒ with the fps. That means, when a
fps is two times higher then another, the speed will be two times slower. The
thing is: there are twice as many frames, so when the speed in every frame is
half as high, the speed per second will be the same.
Using time based motion
When youíve read the
introduction, you know what time based motion is, but not how to use it. Here
you can read that ;). First, you all know this formula, for moving an object in
a straight line, right?
Xposition =
Xposition + Xspeed
Yposition =
Yposition + Yspeed
Now, when
we do time based motion, we do this :
Xposition =
Xposition + Xspeed * time
Yposition =
Yposition + Yspeed * time
Where time is the time that is passed since last frame. When you want to use this formula
in your program, you have to give up the speed in pixels per second, instead of
pixels per frame. When youíre having problems with low speeds, use either fixed
point math or floating point math. This is needed,
because if you run your game at fast computer which run your game at letís say
100 fps(this is very high but for a simple game good
possible), and you have an object that moves at 50 frames per second. That
makes 50/100=0.5 pixels movement per frame. That doesnít work when you use
integers, cause they work only with whole numbers. 0.5
is for an integer the same as 0. The solution? One:
Use floating point(singles). Two: Use fixed point
math. That means: multiply the number(0.5 here) by a
value, for example 10. Then you have 5. Later, when you calculate the position,
integer divide by 10 again. The bigger the number you multiply and divide with,
the bigger the accuracy. For instance, when you multiply by ten, only the first
number behind the dot is saved. When you use 100, the first 2
numbers after the dot. Of course you can use all numbers instead of
tenís and hundredís, you can choose every number you
want. One thing to keep in mind is that the final number (here: 0.5 x 10 = 5)
may not exceed 32767. So when you have coordinates between 0 and 319, you can
multiply with hundred.
To know
what value to give to timer:
Timegone! =
(Lasttimer! - TIMER)
Where
Lasttimer! Is the value of TIMER in the past frame(You
have to save it in an variable).
How a time based motion
engine should look
Hereís some
pseudo code for a time based motion engine.
<code>
Begin of
loop
† Calculate how much time is gone since the
last timer save
† Save the value of the timer
† Draw everything
† End of loop
</code>
Easy, huh?
Problems and possible
solutions
When you
use time based motion you can face some serious problems. The main one is when
you have a TIMER with not enough accuracy. The solution to this is to use
Freebasic. This has a much better timer. With Qbasic, it is hard (or not
possible) to get more accuracy timing.
You get
another problem when you want to run your game at very slow computers. When the
frame rate is low, the speed in pixels per frame is high. This is not good,
since you canít control and see everything well when everything moves too much
between two frames. The solution is just to set a maximum to the time
difference. What I mean is that you say: if the difference in time between two
frames is too high, act like the difference in time is the maximum. By
carefully choosing the maximum number you can get good(but
slower, because you donít use time based motion correctly) results.
A problem
that I already faced, is the inverse: the speed per
frame is very low due to the high framerate. I told you already that you should
use floating point math or preferably fixed point math. When you multiply by
hundred, and run at 100fps, a speed of 1 pixel per second is okay. And that is
very slow. Anyway, when youíre still having troubles (I canít imagine that, but
okay), you can use long type variables and multiply and divide by a much bigger
number, or just use floating point math(but that is much slower then integers
or long integers).
Part 2 - Collision detection
† By RubyNL
Introduction
Collision
detection in something very important in almost all action games. It is VERY annoying when the collision
detection sucks (that means that your bullets are going straight through the
enemies but they stay alive ;)). Collision detection is also fairly easy to do,
if you know how to. I think this tutorial is an absolute must when you want to
program an action/shooting game but you donít know about collision detection
;).
Collision detection
needs to be done:
To check if the
hero/controlled object hits anything,
To check if your
bullets/projectiles hit an enemy or destroyable object
Collision needs to be
done every frame to make sure that objects with an
high speed miss another object. Another solution is to do a line check. You
check if the line between the old object position and the new one intersects
any other lines from objects. This is quite hard to do(I
actually have no clue how to ;) and you can do it either in this way, so Iíll
learn you only this one.
That is for a simple
game. For a complex game, you need to check much more (about anything that is
moving or can move). I will teach you three kinds of collision detection:
† (Non-rotated) square objects
† Spheres
† Per pixel detection
Itís all simple,
except the square-sphere collision detection which is a bit tricky. Iíll start
with squares because they are the simplest.
Collision detection of squares and
spheres
Square objects
Point-square collisions
Point-square
collisions are really easy to check. Squares are defined of two points(like you draw them with line):
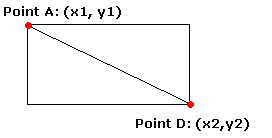
A point is in the
square (so there is a collision) if its x coordinate is between x1 and x2 AND
if its y coordinate is between y1 and y2.
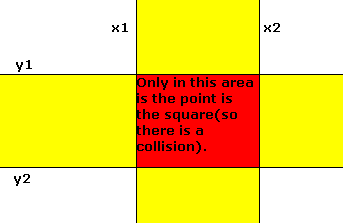
To check if the
x-coordinate is between x1 and x2, just use:
<code>
IF pointx >
squarex1 AND pointx < squarex2 THEN
</code>
Where pointx is of
course the x coordinate of the point to check and squarex1 and squarex2 are the
coordinates of the two points where the square is made from.
This is exactly the
same for the y coordinate. When you have a point at (pointx, pointy) and a
square defined by (dqaurex1, squarey1)-(squarex2, sqaurey2), you can do
point-square collision detection with:
<code>
IF pointx =>
squarex1 AND pointx =< squarex2 AND pointy => squarey1 AND pointy =<
squarey2 THEN Ö
</code>
Well, then you have an
intersection :P. By the way:
Be sure that squarex2
> squarex1 and squarey2 > squarey1.
Else, the intersection
messes up (it will never happen). You can swap the values if squarex1 >
squarex2 or squarey1 > squarey2. Code for this is:
<code>
IF squarex1 >
squarex2 THEN SWAP squarex1, squarex2
IF squarey1 >
squarey2 THEN SWAP squarey1, squarey2
</code>
When I think about it:
this is very much like the classic way of keeping a moving pixel in the screen.
That is: Do separate a check for the x-axis and the y-axis. When it is out of
the screen, invert the horizontal or vertical speed of the pixel.
<code>
IF pointx >
screenxlimit OR pointx < 0 THEN xspeed = -xspeed
IF pointy >
screenylimit OR pointy < 0 THEN yspeed = -yspeed
</code>
That should do it. Of
course you can replace screenxlimit, screenylimit and the two 0ís by variables
that represents the edge of a square or a viewing screen (that could be another
size †then the
real screen).
Square-square collisions
Square-square
collisions are almost as easy as point-square intersections. First, you need to
get four points instead of two for the square. We will check all this points
for intersections.
This image will show
you how to get these four points(point A-D in the
image) from two points(point A & D in the image):
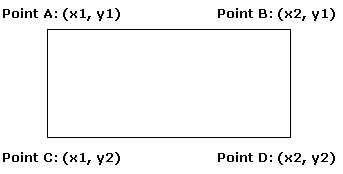
pointax = squarex1
pointay = squarey1
pointbx = squarex2
etc.
Now you just check for
each point (A-D) if itís in the square. Just do a point-square collision. If
one of the four points is in the square, there is a collision. That was all
about it for square objects. Letís move on the round objects!
Spheres
Point-sphere collision
Sphere objects are
checked in a simple, but complete different way then squares. Instead of
checking if a point is between two axes, you need to calculate the distance.
But first assume this object, a nice UFO:

To do collision
detection for a round object, you need to know its radius:

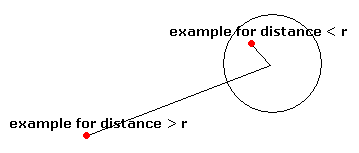
Well, when you need
the radius, all you further need to know to check if a point is its distance to
the center of the sphere. That is done like this:
distance = SQR((pointx - spherex) ^ 2 + (pointy -
spherey) ^ 2)
(Pointx, spherex,
pointy and spherey can all be swapped in the equation, donít worry about that) When
the distance is less then the radius of the sphere, there is a collision.
IF distance =<
radius THEN Ö
But, as some of you
may know: a square root(SQR, used to calculate the
distance, has nothing to do with squares ;)) is very slow. We can optimize this
by squaring both the distance and the radius. It is also faster to multiply(x *
x) then to square(x ^ 2), and be sure to precalculate (r * r) for all the
spheres with a different radius. So we get:
<code>
r2 = r * r
xd = (pointx - spherex)
yd = (pointy - spherey)
distance = xd * xd + yd * yd
IF distance < r2
THEN Ö
</code>
That is fully optimized
point-sphere collision detection. On to the sphere-sphere
collision detection. Itís almost the same as point-sphere collision
detection.
Tip: I am teaching you
how to do a collision detection for perfect round
spheres, but this works for ellipses also. You just divide or multiply xd or yd by a number. You can set the x/y ratio also with
the qb command CIRCLE.

Experiment a bit with it, this is handy when you have to corporate ellipses in
your sprites.
Sphere-sphere collision
Sphere-sphere
collision is in fact the same as a point-sphere collision. The only difference
is that the distance between the centers of the spheres is compared with the
sum of the radius of the two spheres. If you donít understand, this picture
will show you:
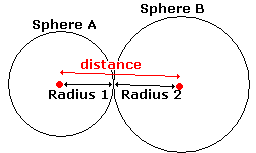
So, together with the optimizations
from the point-sphere collision, that makes (Iíve token sphere A and sphere B):
<code>
r2A = rA * rA
r2B = rB * rB
xd = (sphereAx - sphereBx)
yd = (sphereAx - sphereBx)
IF xd * xd + yd * yd
< r2A Ė r2B THEN ...
</code>
This is it. When you
understand this, you can go on to the tricky square-sphere collision detection.
Square-sphere
collision
Square-sphere
collision is tricky because there can be two types of collision. The first is
what I call a straight intersection, where the sphere Ďhitsí the square on a
side. Then you have the Ďcornerí intersection, where the sphere hits a corner
of the square.

To know for which type
of collision we have to check, I first look where the center of the sphere is.
This is a picture from the point-square check:

Consider the red area
as the square. If the center of the sphere is in the red area, there has to be an collision. If the center is in the yellow area, we have
to check for a straight intersection. If the center is in the white area, we
check for a corner intersection. But before we check, we decide in which area
the center of the sphere is.
I assume a sphere
(spherex, spherey, radius) and a square(squarex1,
squarey1)-(squarex2, squarey2).
For this I made a
table. I assign 1 to a variable called xc if the
center of the sphere is less then squarex1. If the center is between squarex1
and squarex2 I assign 2 to it, and else(it is more
then squarex2) 3. For y-axis I do the same. Code:
<code>
IF spherex <
squarex1 THEN
† xc = 1
ELSEIF spherex <
squarex2 THEN
† xc = 2
ELSE
† xc = 3
END IF
IF spherey <
squarey1 THEN
† yc = 1
ELSEIF spherey <
squarey2 THEN
† yc = 2
ELSE
† yc = 3
END IF
</code>
Then we lookup what to
do with this table:
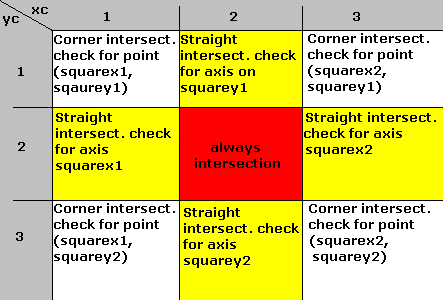
A corner intersection
check is just a normal point-sphere collision
detection. As point you take the closest corner point and as sphere the sphere
where you are doing the check on.
A straight
intersection check is the Ďstraightí distance between the center and an edge.
(I referred to the
edge as Ďaxisí in the table). A picture and some code
for this:
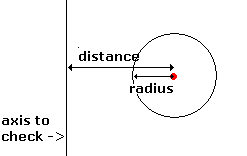
<code>
distance =
ABS(spherex Ė squarex1)
</code>
Note: when you use
ellipses instead of circles, be sure that you divide or multiply the x/y
coordinate here too.
The code
for a square-sphere collision detection(after you
assigned values for xc and yc):
(This code
is only to show you how it should be used and interpreted: I wrote it down from
my head, so there may be some bugs)
<code>
intersection = 0
IF xc = 1 THEN
† IF yc = 1 THEN intersection = cornercheck(squarex1, squarey1, spherex, spherey, radius)
† IF yc = 2 THEN intersection = straightcheck(squareyx1, spherex, radius)
† IF yc = 3 THEN intersection = cornercheck(squarex1, squarey2, spherex, spherey, radius)
ELSEIF xc = 2 THEN
† IF yc = 1 THEN intersection = straightcheck(spherey, squarey1, radius)
† IF yc = 2 THEN intersection = 1
† IF yc = 3 THEN intersection = straightcheck(spherey, squarey2, radius)
ELSE
† IF yc = 1 THEN intersection = cornercheck(squarex2, squarey1, spherex, spherey, radius)
† IF yc = 2 THEN straightcheck(squareyx2,
spherex, radius)
† IF yc = 3 THEN intersection = cornercheck(squarex2, squarey2, spherex, spherey, radius)
END IF
FUNCTION cornercheck(pointx, pointy, spherex, spherey, radius)
xd =
(pointx - spherex)
yd =
(pointy - spherey)
r2 = radius
* radius
distance
= (xd * xd + yd * yd)
IF distance
<= r2 THEN cornercheck = 1 ELSE cornercheck = 0
END
FUNCTION
FUNCTION straightcheck(edgec, spherec, radius)
straightdistance = ABS(spherec - edgec)
IF
straightdistance => radius THEN straightcheck = 1 ELSE straightcheck = 0
END
FUNCTION
</code>
Optimization
trick:
When you
have a TYPE specially for a circle, consider adding r2
to it: the square of the radius:
<code>
TYPE sphere
† Centerx as integer
† Centery as integer
† Radius as integer
† R2 as integer
End type
</code>
When you do
this, r2 doesnít have to be calculated during the collision detection.
How to corporate spheres
and squares into sprites
I first
assumed that all the sprites you used are:
1. Just
circles and squares drawed with qbís line and circle or
2. Perfect
round or square.
I thought
that people may want other shapes as well :P. So here
is a lil text for when you have a sprite that is not quite round or square but
you donít want to use per pixel checking.
Letís start
with this paddle, I made for possible use in a
Pong-like game: 
This is not
a sphere, but neither a square. To still have a correct collision, we split it
up into two spheres and one square:
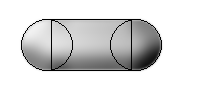
Iíve got to
tell you one thing on collision detection when you want to bounce a ball on
some object. You might want to check every position of the ball where it
current is, and when it has a collision, bounce it. This is wrong. What you
need to do is bounce actually before there is an
collision. So you need to check what the new position would
be if there wouldnít be a collision. If there is a collision at THAT
place, then bounce. So actually the ball never has a collision because it bounces
before it has a collision. This may sound stupid, but when you check after you
updated the position, and there is a collision and you draw it, you draw the
object over another(while it should bounce off it).
Here is
another sprite:

We can
split this shape up into this:
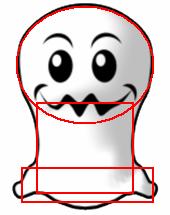
You see
that it impossible to exactly fit the sprite in the spheres and squares without
using a huge amount of squares/spheres. You can give it your best try, or you
can use pixel perfect manner, which is a bit harder to use.
Pixel perfect collision
detection
Pixel
perfect collision detection allows you to use complex sprites and still have
precise collision detection. This manner is called Ďpixel perfectí because you
have to check for each pixel. This could make it slow, but when you optimize it
well it will be worth it. There are two different manner
that Iíll explain to you. The first is based on colour checking.
Colour checking
I will
directly introduce the downside of colour checking: you have to divide your
palette in different Ďareasí. For example:
0-127
Background colours
127-150
Character colours
150-200 Bullets
and booby traps colours
200-255
Object colours
When you draw everything to your buffer in a fixed sequence(background,
powerups, enemies), you draw everything except the character. Instead of just
drawing it, you check the colour of every pixel before you over paint it.
Then you lookup what to do with that colour. For instance (using the table above,
of course you could make your own ;)), when a colour
is 0-127 you donít have to anything, because that are background colours. But,
when a colour is from 150 to 200, you know that the hero is hit by a bullet or
booby trap. This is the essence of the colour checking method. If you want, you
could make a lookup table for every colour where is saved what to do with that
single colour (subtract a life, game over, extra health, etc). This is the easy
variant of pixel perfect collision detection.
Array checking
Array
checking is a good method when you want to use more colours in your sprite,
instead of having a limited amount of colours that you can use for the
background, your character, etc. Instead of painting except the hero, you paint
the hero, and keep an array of points which will be checked for collision. Now
when you paint the other sprites, you check if they are on any of the points in
the array. This is all about array checking. It sounds simple, but it is
actually a lot of work to code.
Some notes on optimization
The pixel
perfect manner is slow when you use the array checking method. To make it
faster you do the Ďbounding boxí optimization like I told you above. Checking
for one box is faster then to check for all pixels of the hero. This shouldnít
be done for each pixel of the sprite, so donít use a point-square
collision detection but a square-square collision detection. If there is a
collision, then check for each pixel if it is one of the coordinates stored in
the array.
A bounding
box is also useful if you have a sprite that consists out of more then tree pieces(spheres or squares).
Also, you
can get the whole thing faster, always use as much
integers as possible for everything! When youíre getting overflow errors, try
too use LONG type variables. This is very much faster
then singles. Singles are only needed when you need much accuracy. Examples are
ray tracers, fractals and sometimes for speeds(very
slow rolling balls, less then one pixel per frame).
Well, this
was all I know about collision detection. Succes with using it, and I hope this
tutorial helped you. Else, mail me! For other tutorials, check out my website: http://members.lycos.nl/rubynl.
RubyNL