By Matthew R. Knight <horizonsqb@hotmail.com>
Briefly, trigonometry is the study of the relations that exist between the sides and angles of every triangle. Imagine you have a triangle and you only know the length of one of its sides and the size of one of its angles. With trigonometry you can easily find all the other sides and angles of that triangle. So in other words, with trigonometry you can solve a triangle that you know very little about.
Trigonometry is a subject of great scope. I won't be covering the whole subject in this tutorial, but the fundamental building blocks discussed here will help get you started.
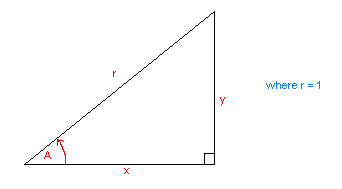
In the graphic below, it can be seen that there is a fixed ratio between the sides of a right-angled triangle, provided the angle does not change.
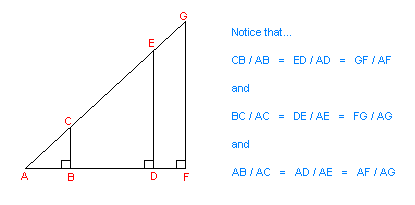
Congratulations! You have just learned the most fundamental and important law in trigonometry: The quotient of the ratio of any two sides in a right- angled triangle is fixed, provided that angle A remains the same. A proof of this law will be provided later in this tutorial.
Mathematicians have given names to each of the possible ratio's of a right- angled triangle. They are as follows:
The ratio's each of the above represent are as follows:
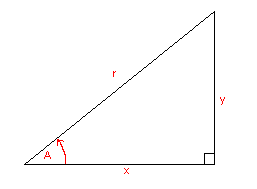
sin(A) = y/r cosec(A) = r/y cos(A) = x/r sec(A) = r/x tan(A) = y/x cot(A) = x/y
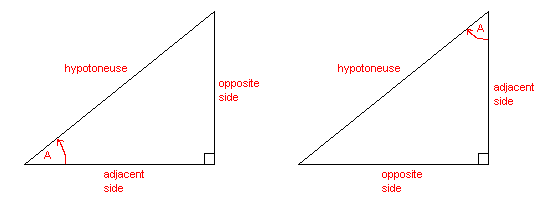
sin(A) = y/r = opposite side/hypotoneuse cos(A) = x/r = adjacent side/hypotoneuse tan(A) = y/x = opposite side/adjacent side cosec(A) = r/y = hypotoneuse/opposite side sec(A) = r/x = hypotoneuse/adjacent side cot(A) = x/y = adjacent side/opposite side
Any right-angled triangle may be solved if the following information is given:
and/or
Here's some examples of triangles solved with trigonometry...
In triangle ABC we have C = 90 degrees, B = 35 degrees and BC = 30mm. Find the length's of AC and AB.

AC/BC = tan(35 degrees) -> AC = BC * tan(35 degrees)
Using a scientific calculator, we find tan(35 degrees) is equal to 0, 700.
-> AC = 30 * 0, 700 -> AC = 21mm
Easy huh? Now we will find AB...
AB/BC = sec(35 degrees) -> AB = BC * sec(35 degrees)
Once again, we use our scientific calculator. We find that sec(35 degrees) is equal to 1, 221.
-> AB = 30 * 1, 221 -> AB = 36, 6mm
Now wasn't that simple? :) Let's try another example...
In triangle PQR we have R = 90 degrees, QR = 27mm and PR = 43mm. Find Q.
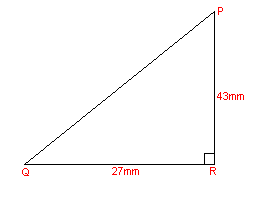
tan(Q) = 43/27 -> tan(Q) = 1, 593
Now we use our scientific calculator to find what amount of degrees corresponds with 1, 593. We use the 1/tan button on the calculator, and find it to be 57, 9 degrees...
-> Q = 57, 9 degrees
Isn't trigonometry easy? :)
Notice that we have used a calculator throughout these examples to find various values. For example, we used the 1/tan button on the calculator to get the angle in degrees of Q from the quotient of the tangent to that angle.
But what if we don't have a calculator?
By building a table of values that would result from every angle for each of the trigonometric functions, we could easily have looked up the value "1, 593" in the "tan" column, and then found the corresponding angle. This is really simple in concept, but building a complete trig. table would take ages, so just save yourself a lot of trouble and use your calculator! :)
We have learned that the entire subject of trigonometry rests on the following simple but important fact:
The quotient of the ratio of any two sides in a right-angled triangle for a certain angle A is fixed.
But why is this so? There must be a reason. I have managed to prove this on my own. It's probably not the best proof, so if you know of a better method please let me know.
Consider the following:
If we multiply r by 2, r = 2. Multiply it by 3, r = 3. And so on. This should be pretty obvious I think! :)
x can be viewed as the horizontal component of vector r, and y can be viewed as the vertical component of vector r.
We know from Pythagoras' theorem that: r^2 = x^2 + y^2. This can also be represented as:
(r * r) = (x * x) + (y * y)
Let's say that r in our diagram was twice as long...
2 * (r * r) = 2 * [(x * x) + (y * y)] (2r * 2r) = (2x * 2x) + (2y * 2y) -> 4r^2 = 4x^2 + 4y^2
It is evident from the above that if r is multiplied by Z, the length's of x and y will then be x * Z and y * Z respectively.
We can thus conclude that:
r/x = Zr/Zx -> r/x = r/x -> 1 = 1
We can prove every other trigonometric ratio similarly.
We've come to the end of this tutorial. You've learned a lot, and now I'll leave you to experiment with your new knowledge. There's a lot more to trigonometry than what I've shown you here today... If anyone would like me to write about this stuff, just drop an e-mail my way.