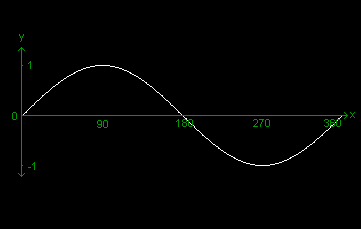
Writer: Matthew R.Knight

In spite of the fact that QB is poorly equiped in terms of graphics capabilities, with some ingenuity, very impressive effects can be created. This tutorial will cover the theory behind creating a plasma-like effect in QB. Enjoy!

In order to produce some plasma-like patterns we can use the Sine wave. The Sine wave is of course the graph of the trigonometric function: SIN. A Sine wave may be plotted on the Cartesian Plane by using the equation y = SINx.

The properties of the Sine wave are as follows:

* The graph reaches no height greater than 1, and no height lower than -1. The line y = 0 is the middle of the wave - In other words, the x-axis of the Cartesian Plane is the middle of the wave in terms of height.

* The period (width) of the wave is 360.

* The wave is above the line y = 0 where: 0<x<180 (1st and 2nd quadrants.)

* The wave is below the line y = 0 where: 180<x<360 (3rd and 4th quadrants.)

We can get the height (y coordinate) of the wave at any of the 360 points of its width by using QB's SIN function. However, we must bear in mind that the SIN function requires the angle argument to be in radians. Since it is simpler and more natural to think in degrees, we can perform a simple conversion...

Radians = Degrees * 0.017453

So, to get the Y position of the sine wave at 90 degrees we would use this:

PRINT SIN(90 * 0.017453)

This is what the Sine wave looks like when plotted on the Cartesian Plane:

It may have occured to you that we could plot the Sine wave on the screen, using some simple BASIC code. There's a bit of a problem though. The amplitude (height) of the wave is 1. This means that each y-coordinate will be either 1 or a fraction of 1, and since 1 is the same as one pixel, we'll end up with a straight line! :(

Of course we could use some multiplication and addition to make the amplitude bigger. In fact, we can make the amplitude whatever we want! The following code makes the wave have an amplitude of 50, with y = 50 the mid-point.

PRINT (SIN(degrees% * 0.017453) * 50) + 50

Now we can plot our Sine wave on the screen! The following code does this for us:

SCREEN 13

FOR x% = 0 to 360
  PSET (x%, (SIN(x% * 0.017453) * 50) + 50), 15
NEXT x%

You have probably already noticed that there's a major problem with the code above. A Sine wave is 360 degrees wide but SCREEN 13 is only 320 pixels wide, which means that some of the wave will be left out. To fix this all we have to do is scale down the x% variable into another variable called xx%.

SCREEN 13

FOR x% = 0 to 360
  xx% = (x% / 360) * 320
  PSET (xx%, (SIN(x% * 0.017453) * 50) + 50), 15
NEXT x%

If you run the code above you'll notice the Sine wave goes from the middle to a trough, then up to a peak, and then back down to the middle. If you look at our picture of the Sine wave plotted on the Cartesian Plane you'll notice that QB has plotted the wave the wrong way round. This is because on the Cartesian Plane Y extends positively upwards, and on our screen, Y extends positively downwards. This is easy to fix. Simply multiply each Y coordinate by -1.

Okay, cool. Now we have a Sine wave. The wave has an amplitude of 50. The wave also has a property known as frequency, which is basically how many Sine waves we can fit in a certain amount of space. If there were two Sine waves plotted on the screen instead of one, we say that it has a frequency twice as large.

Just for fun, let's try mix Sine waves. For example, we can mix Sine waves that have different frequencies. Before we do this, let's simplify our last program a little:

SCREEN 13

FOR x% = 0 to 360
  xx% = (x% / 360) * 320 
  rad = (x% * 0.017453)
  srad = SIN(rad)
  PSET (xx%, (srad * 50) + 50), 15
NEXT x%

The above program will work exactly the same as the last one. All we did was neaten the code a little, and make it easier to mix the two waves. Right, now we want to mix two Sine waves... Erm, how do we do that??!! It's very simple really. What we do is take our normal Sine wave and mix it with one which has a higher frequency. We do this by taking the line:

srad = SIN(rad)

which only creates a single wave and add another wave with a different frequency to it, and then average out the pair...

srad = (SIN(rad) + SIN(rad * 2.8)) / 2

In making that adjustment, you'll end up with a wave that has more "random" amplitudes. Looks pretty cool no? Try adding several other waves and see what happens! Go on! ^_^

Another good adjustment you could make to the program is the addition of a lookup table for the SIN values. This will make the proggy run significantly faster! ^_^

A lookup table can be constructed by creating an array holding the SIN values for 0 to 360. Then instead of calling the SIN function you just retrieve the value from your array.

Now at this point you're probably wondering what all this has to do with colorfull patterns and plasma right? Well, the Sine waves can be used to create interesting palette setups. To be able to demonstrate this better let's adjust the program to create waves of amplitude = 63. And what else has a maximum value of 63? Right! Each palette-index hue.

SCREEN 13

FOR x% = 0 to 360
  xx% = (x% / 360) * 320
  rad = (x% * 0.017453)
  srad = (SIN(rad) + SIN(rad * 2.8)) / 2
  PSET (xx%, (srad * 31) + 31), 15
NEXT x%

Now let's use this wave to adjust the palette in colors 1 to 100.

SCREEN 13

FOR x% = 0 to 360
  xx% = (x% / 360) * 100 'notice the change to 100 here.
  rad = (x% * 0.017453)
  srad = (SIN(rad) + SIN(rad * 2.8)) / 2
  OUT &H3C8, xx% + 1
  OUT &H3C9, (srad * 31) + 31
  OUT &H3C9,0
  OUT &H3C9,0
NEXT x%

Now that creates a very nice palette indeed. Of course you now want to see it in action! Add the following code to the end:

FOR x% = 1 TO 100
  FOR y% = 1 TO 100
    PSET (x%, y%), (x% + y%) / 2
  NEXT y%
NEXT x%